슬릿들의 간격과 위치를 조절할 수 있습니다.
영의 이중 슬릿 실험
Young의 간섭 실험은 다음과 같습니다. 스크린 A의 작은 구멍 S0에서 회절된 빛이 스크린 B에 있는 작은 구멍 S1과 S2를 지나게 됩니다. 두 개의 작은 구멍을 지난 빛이 스크린 B와 C사이에서 중첩되어 스크린 C에 간섭무늬를 만듭니다.
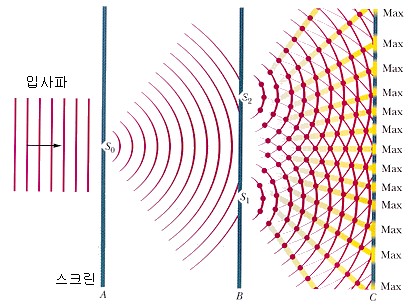
두 슬릿으로부터 도착한 파가 위상이 같을 때 밝은 무늬가 생기고 위상이 같지 않은 파가 겹칠 때 검은 무늬가 생깁니다.
보강간섭
스크린에서 같은 위상이 도달하는 부분은 ‘보강간섭’이 일어나서 밝게 보입니다.
보강간섭을 일으키기 위해서는, 경로차인 d·sin θ 가 ‘0’ 또는 파장의 정수배가 되어야 합니다.
d: 슬릿의 간격(m)
θ: 회절 각(rad)
λ: 빛의 파장(m)
D: 슬릿으로부터 스크린까지의 거리(m)
‘n = 0’일 때 중심축의 회절각 ‘θ = 0’입니다. 결국 중심축 은 스크린의 중심에 있습니다.
상쇄간섭
스크린에서 어두운 지역에서는 ‘상쇄간섭’이 일어납니다.
상쇄간섭을 일으키려면 두 빛의 경로차가 반파장의 홀수배여야 합니다.
d: 슬릿의 간격(m)
θ: 회절 각(rad)
λ: 빛의 파장(m)
D: 슬릿으로부터 스크린까지의 거리(m)
위의 ‘n’값은 상쇄간섭에 의한 어두운 무늬에 번호를 매길 때 사용합니다.