꼬마도 알고 있는 그네 타기의 비법
“어떻게 그렇게 높이 올라갈 수 있니?”
세상에는 누구나 알고 있지만, 그 원리를 말로 설명하기 힘든것이 있습니다.
그 중의 하나가 그네 타는 방법이라고 생각합니다.
그네 타는 방법을 물리적으로 설명할 수 있을까요?
움직이는 그네의 중간 지점에서 일어서거나 앉으면 진자의 길이가 변합니다.
즉, 그네는 ‘길이를 변화시킬 수 있는 진자‘로 생각할 수 있습니다.
아래 그림과 같이 운동하는 진자의 길이가 중간에 바뀌는 경우를 생각해 봅시다.
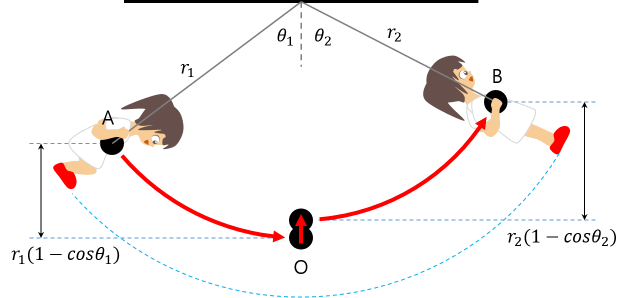
A → O로 내려가는 경우
감소한 위치 에너지는 증가한 운동 에너지와 같습니다.
\[ mg r_1 (1 – cos \theta_1 ) = \frac{1}{2}mv^2 \\ v^2 = 2gr_1 (1 – cos \theta_1 ) \]
O → B로 올라가는 경우
감소한 운동 에너지는 증가한 위치 에너지와 같습니다.
\[ \frac{1}{2}mv^2 = mg r_2 (1 – cos \theta_2 ) \\ v^2 = 2gr_2 (1 – cos \theta_2 ) \]
A → B로 이동하는 동안 각도의 변화
O점에서의 속력은 변하지 않으므로,
\[ 2g r_1 (1 – cos \theta_1 ) = 2g r_2 (1 – cos \theta_2 ) \\ r_1 (1 – cos \theta_1 ) = r_2 (1 – cos \theta_2 ) \] \[ \therefore \theta_2 = cos^{-1} ({\frac{r_2 – r_1(1 – cos \theta_1)}{r_2}}) \]가 됩니다.
그네를 잘 타기 위한 방법은?
내려갈 때 r의 길이를 증가시켜야 합니다. (즉, 앉습니다.)
반대로 올라갈 때는 일어서면 됩니다.
예를 들어, 다음과 같은 조건을 대입해서 각도의 증가량을 계산해 보겠습니다.
- \( r_1 = 3m \)
- \( r_2 = 2m \)
- \( \theta_1 = 45˚ \) (출발 지점의 각도)
\[ \begin{align} \theta_2 &= cos^{-1} ({\frac{r_2 – r_1(1 – cos \theta_1)}{r_2}}) \\ &= cos^{-1} ({\frac{2 – 3(1 – cos 45˚)}{2}}) \\ &\approx 55.9˚ \end{align} \]
이 경우, 각도가 약 1.24배 증가합니다.