피타고라스의 정리는
직각삼각형의 3개의 변을 a, b, c라고 하고 가장 긴 변을 c라고 할 때, 피타고라스의 정리는 방정식 a2 + b2 = c2가 항상 참이 된다는 것입니다.
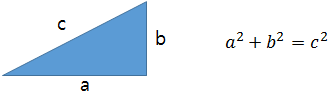
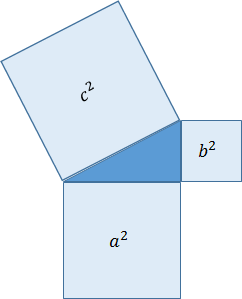
한 변의 길이가 각각 a, b, c인 정사각형의 넓이는 a2, b2, c2이 되므로, 방정식 a2 + b2 = c2은 각각의 변을 이용하여 만든 세 정사각형을 가정할 때 작은 두 정사각형의 넓이를 합하면 큰 정사각형과 같습니다.
피타고라스는 기원전 500년경에 살았던 고대 그리스의 철학자입니다.
기록에 따르면 피타고라스의 정리는 피타고라스가 발견한 것이아닙니다. 피타고라스가 태어나기 이전부터 고대 이집트나 중국 등 세계 곳곳에서 이미 같은 개념이 알려져 있었고 건축, 측량 등에 사용되기도 했습니다.
그럼에도 이 개념이 ‘피타고라스의 정리’라는 이름으로 전해진 것은 유클리드가 쓴 기하학 책에서 비롯된 것으로 알려져 있습니다. 피타고라스의 정리는 유클리드가 쓴 ‘원론’에 기록돼 있고, 이 원론은 유럽에서 2000년 이상 수학교과서처럼 사용했습니다.
피타고라스 정리의 응용
자바실험실을 만드는 과정에 피타고라스의 정리가 자주 사용되었습니다.
예를 들어, 화면상에 위치한 두 점 사이의 거리를 알아내는 방법은 피타고라스의 정리를 이용한 것입니다.
