인공위성의 원리

포탄이 인공위성이 되려면?

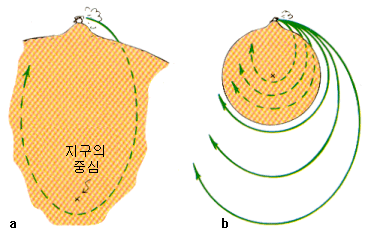
a. 포탄이 포물선을 그리며 낙하한다고 생각해 봅시다. 포탄이 그리는 궤적은 사실 지구 중심을 초점으로 하는 타원궤도의 일부분입니다. 지구의 중심은 타원의 먼 초점에 해당합니다.

b. 포탄이 지표면과 충돌하지 않으려면 최소한 8km/s(정확히 7920m/s)의 속도로 지표면과 수평으로 발사되어야 합니다. 속도가 이보다 더 빨라지면 지구의 중심점을 타원의 가까운 초점으로 하는 타원운동을 합니다.

슈퍼맨이 던진 인공위성

슈퍼맨이 높은 산위에서 돌을 던진다고 할 때 어떤 속도로 던지느냐에 따라 다양한 운동을 합니다.

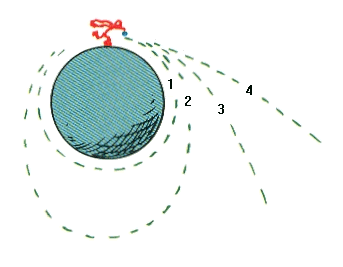
≒ 8km/s
지구표면곡률과 일치하여 원형궤도를 돕니다. 단, 지구의 굴곡에 부딪치거나 대기와의 마찰이 없다는 가정하에서만 가능합니다. 던져진 공은 90분 후에 지구를 한바퀴 돌고 제자리로 돌아옵니다.
< 11.2km/s
타원궤도를 돌며 돌아오는데에는 90분이 넘게 걸립니다.
≒ 11.2km/s
쌍곡선 궤도를 그립니다. 더 빠른 속력으로 던진다면 공은 다시 돌아오지 않습니다.
> 11.2km/s
지구를 탈출할 수 있습니다.
> 42.5km/s
태양계를 탈출할 수 있습니다.

구심력, 인공위성이 회전하도록 하는 힘

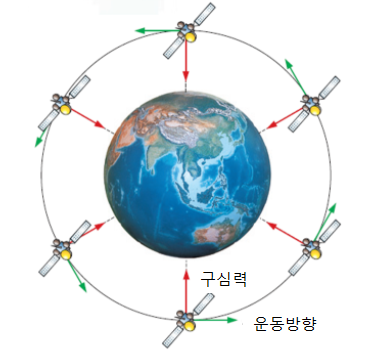
눈에는 잘 보이지 않지만, 현재 지구 위에는 수많은 인공위성이 돌고 있는데, 이 인공위성은 지구 주위의 일정한 궤도로 등속원운동을 하고 있습니다.지구가 인공위성을 잡아당기는 힘인 중력이 바로 구심력이 됩니다.

원 궤도를 유지하기 위한 속도의 계산

반지름이 r인 원형 궤도를 돌고 있는 인공위성에 대해 생각해 보세요.
중력과 구심력이 같다고 생각하면, 인공위성은 원운동을 하게 됩니다.

\[ \begin{align} ( 구심력 &= 중력 ) \\ m\frac { { v }^{ 2 } }{ r } &=G\frac { Mm }{ { r }^{ 2 } } \end{align} \]

\( v =\sqrt { \frac { GM }{ r } } \)\( =\sqrt { \frac { 6.67\times { 10 }^{ -11 }{ m }^{ 3 }/{ s }^{ 2 }\cdot kg \times 5.972\times { 10 }^{ 24 }kg }{ 6.37\times { 10 }^{ 6 }m } } \)\( \approx 7907m/s \)

탈출 속도의 계산

인공위성에 작용하는 위치에너지를 인공위성의 운동에너지로 보상이 된다면 지구로부터 탈출이 가능해집니다.

\[ \begin{align} ( 인공위성의 운동 에너지 &= 위치 에너지 ) \\ \frac { 1 }{ 2 } m{ v }^{ 2 }&=G\frac { Mm }{ r } \end{align} \]

\( v =\sqrt { \frac { 2GM }{ r } } \)\( =\sqrt { \frac { 2 \times 6.67\times { 10 }^{ -11 }{ m }^{ 3 }/{ s }^{ 2 }\cdot kg \times 5.972\times { 10 }^{ 24 }kg }{ 6.37\times { 10 }^{ 6 }m } } \)\( \approx 11183m/s \)

떨어지고 있는 달

사과를 나무에서 떨어지게 하는 힘과 같은 종류의 힘이 달에도 작용합니다.

달은 지구의 중력때문에 1초 동안 1.4mm낙하합니다.