파스칼의 삼각형

파스칼의 삼각형은 수학에서 이항계수(서로 다른 몇 개의 물건 중에서 순서없이 물건을 선택할 수 있는 경우의 수)를 삼각형 모양의 기하학적 형태로 배열한 것입니다.
이것은 블레즈 파스칼에 의해 이름 붙여졌으나 이미 수세기 전에 다른 사람들에게서 연구된 것입니다.
파스칼의 삼각형은 그 안에 수학적으로 흥미 있는 현상들이 많이 숨어 있습니다.

파스칼의 삼각형 만드는 방법

위쪽의 양쪽 사선 방향에서 내려받은 숫자를 서로 더하면 파스칼의 삼각형이 만들어 집니다.
삼각형의 양쪽 빗면의 숫자는 '1'로 합니다.

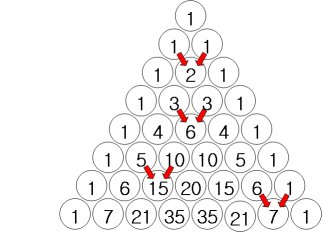
파스칼의 삼각형 특징

각 행의 합은 2의 거듭제곱과 같습니다.
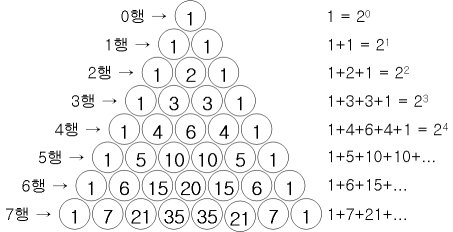
숫자들의 의미 = 위쪽 수열의 합과 같습니다.
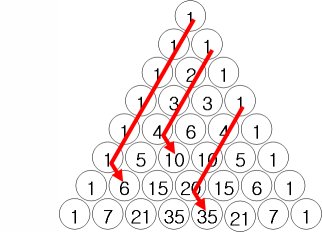
각 열에 나열된 수는 특별한 의미를 가집니다.
제 1열 = 모두 자연수 '1'입니다.
제 2열 = 자연수의 수열
제 3열 = 삼각수(물건을 모아서 정삼각형 모양으로 만들 수 있는 물건의 개수)
제 4열 = 사면체수(물건을 쌓아서 정사면체 모양으로 만들 수 있는 물건의 개수)
피보나치 수열이 됩니다.
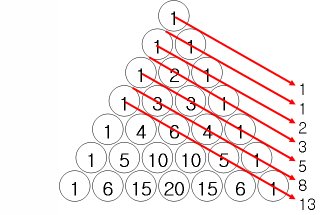
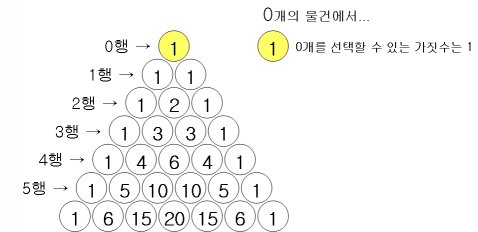
0행의 수열 = 0개의 물건 중에서 순서 없이 물건을 뽑는 조합의 가짓수
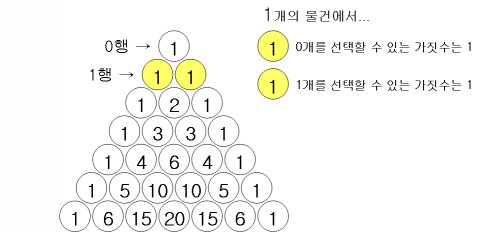
1행의 수열 = 1개의 물건 중에서 순서 없이 물건을 뽑는 조합의 가짓수
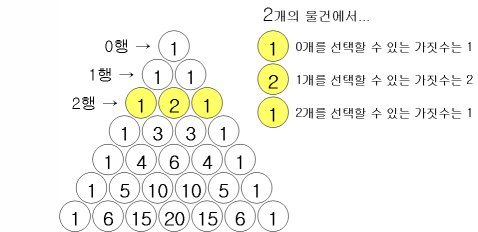
2행의 수열 = 2개의 물건(A, B) 중에서 순서 없이 물건을 뽑는 조합의 가짓수
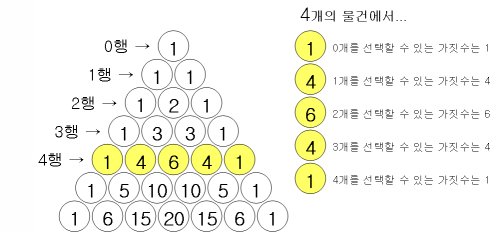
4행의 수열 = 4개의 물건(A, B, C, D) 중에서 순서 없이 물건을 뽑는 조합의 가짓수