실상과 허상
어떤 물체를 보면서, 우리는 그 곳에 물체가 있다고 느낍니다. 그런데 물체나 발광체가 그곳에 없는데도, 어떤 반사체 또는 발광체가 그곳에 있다고 느끼는 경우 우리는 그곳에 ‘상(image)’이 있다고 말합니다.
광학에서 말하는 ‘상(image)’은 빛이 굴절 혹은 반사되어서 생깁니다.
실상(Real image): 실제로 빛이 그곳에서 모였다가 다시 출발하는 경우를 말합니다. 실상이 맺혀지는 위치에 종이를 대보면 종이에 맺힌 상이 실제로 보입니다.
허상(Virtual image): ‘상’이 맺힌 곳에 실제로 빛이 존재하지 않는 경우를 말합니다. 허상이 맺혀지는 위치에 종이를 대보면 아무런 상이 나타나지 않습니다.
볼록 거울의 허상
거울에 나타난 상은 언제나 허상이고, 물체와 같은 모양으로 서있고, 또한 실물보다 작게 보입니다. 넓은 범위를 비춰줄 수 있기 때문에 자동차 백미러나 감시용 거울에 사용됩니다.
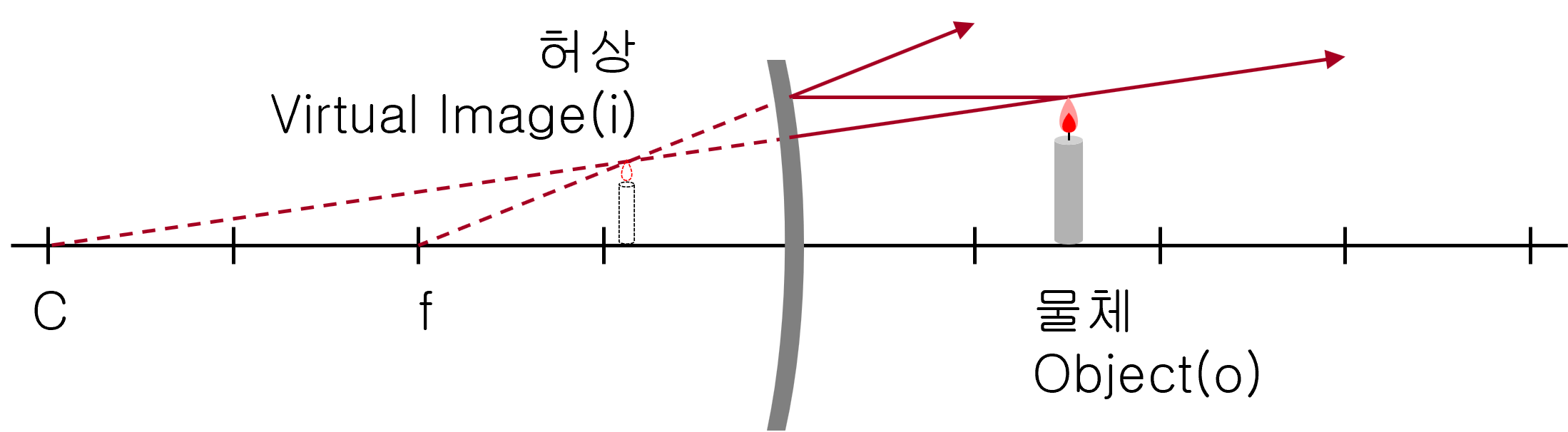
오목 거울의 허상과 실상
오목 거울은 물체가 오목 거울의 초점 거리 안쪽에 있는가 그렇지 않은가에 따라 큰 차이를 보입니다.
물체가 거울의 초점 거리 안에 있을 경우: 허상이며, 물체는 실물보다 확대되어 보입니다. 그리고 항상 똑바로 서있습니다.
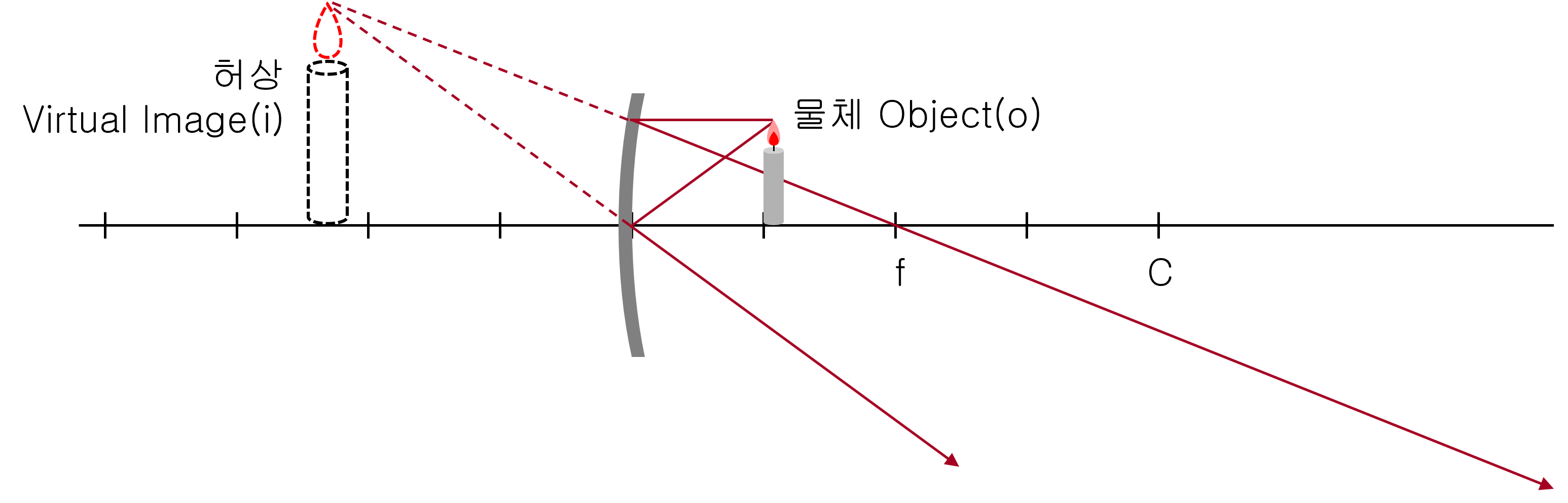
물체가 거울의 초점 거리 밖에 있을 경우: 실상이며, 거울과의 거리에 따라 확대되거나 축소되어 보입니다. 그리고 항상 반전되어 있습니다.
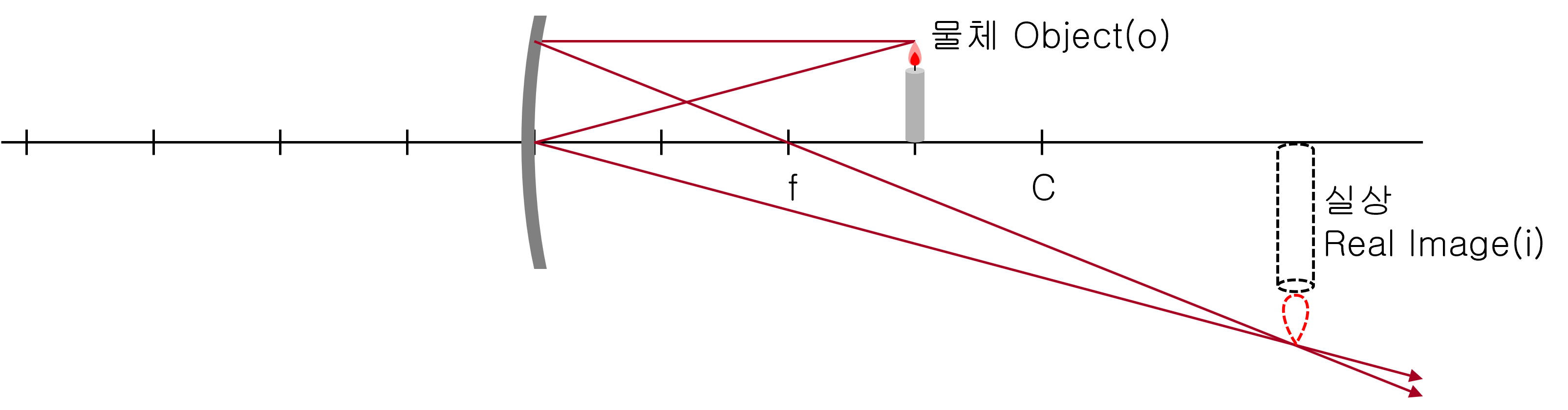
숟가락의 안쪽은 오목 거울, 바깥쪽은 볼록 거울로 볼 수 있습니다.
맺힌 상의 거리 구하기
거울로부터 물체의 거리 o, 거울로부터 상의 거리 i, 그리고 거울의 초점거리 f사이에는 다음과 같은 간단한 공식이 성립합니다.
\[\frac { 1 }{ o } +\frac { 1 }{ i } =\frac { 1 }{ f } =\frac { 2 }{ C } \]
- o: 거울에서 물체까지의 거리. 항상 양(+)의 값을 가집니다.
- i: 거울에서 상까지의 거리
- f: 초점 거리
- C: 구심 거리 (곡률의 중심, 초점거리의 약 2배 거리)
볼록 거울의 경우
- o > 0: 실물체
- i < 0: 허상 (V쪽)
- f < 0: 허초점 (V쪽)
오목 거울의 경우
- o > 0: 실물체
- f > 0: 실초점 (R쪽)
- i = ?: 상황에 따라 다릅니다.
- o < f 인 경우: i < 0 (똑바로 서 있는 허상)
- o = f 인 경우: i 값을 구할 수 없습니다.
- o > f 인 경우: i < 0 (뒤집혀 있는 실상)
광선추적법
어느 두 광선의 경로를 추적하면 맺힐 상을 찾아낼 수 있습니다.
- 중심축에 평행한 광선은 반사 후 초점을 지나 갑니다.
- 거꾸로 생각하면, 초점을 통과한 후 거울에 입사한 광선은 거울을 반사한 후 중심축에 평행하게 진행해 나갑니다.
- 곡률중심 C를 통과한 후 거울에 반사한 광선은 입사 경로를 되밟아 나옵니다.
- 거울의 중심에 입사되는 광선은, 대칭적인 각도로 반사됩니다. (일반적인 반사의 법칙)
배율 구하기
거울에 맺힌 상의 크기 비율은,
\[m=-\frac { i }{ o } \]
- m: 배율
- i: 거울에서 상까지의 거리
- o: 거울에서 물체까지의 거리
계산된 m의 값에따라 상은 다음과 같이 보입니다.
- m > 0: 상은 똑바로 서 있습니다.
- m < 0: 상은 뒤집혀 서 있습니다.
- |m| > 1: 상은 확대되어 있습니다.
- |m| < 1: 상은 축소되어 있습니다.