双子のパラドックス
双子のパラドックスは、特殊相対性理論の「時間の伸び」概念が矛盾を内包しているように見えることから始まりました。
双子のパラドックスは、おおよそ次のような物語で行われます。 (メディアによって少しずつ内容が異なります。)
- 一対の双子のうち、一人は地球に残り、もう一人は宇宙船に乗って地球を去ります。 便宜上、「地球人」と「宇宙人」と呼びます。
- 宇宙船は光速に近い高速で飛行します。
- 宇宙船は10年後に地球に戻ります。
10年後、双子がお互いに会ったとき、誰がもっと老化していますか?
- 地球人の立場で地球は停止しています。 つまり、宇宙人の位置が変化したので、宇宙人の時間がゆっくりと流れます。 そのため、宇宙人に比べて地球人がより老化しているはずです。
- 宇宙人の立場では、地球は非常に速い速度で宇宙船から離れる。 したがって、地球の時間がゆっくりと流れます。 ですから、地球人に比べて宇宙人がより老化しているはずです。
双子のパラドックスの解決
双子のパラドックスは、ミンコフスキーの4次元時空間で解決できます。
ミンコフスキー時空間の詳細については、次のリンクを参照してください。
ミンコフスキー空間を導入するときは、次の点に注意してください。
- 観察者は、それぞれの座標系に基づいて周囲のものを観察します。
- 光の速度はどの座標系でも同じです。
- 光の速度が同じであるため、座標系の軸は曲がったり傾いたりすることがあります。
宇宙船が離れるだけの場合
宇宙船が戻らずに遠ざかる場合を考えてみましょう。
前述のように、観察者はそれぞれの座標系に基づいて周囲のものを観察します。
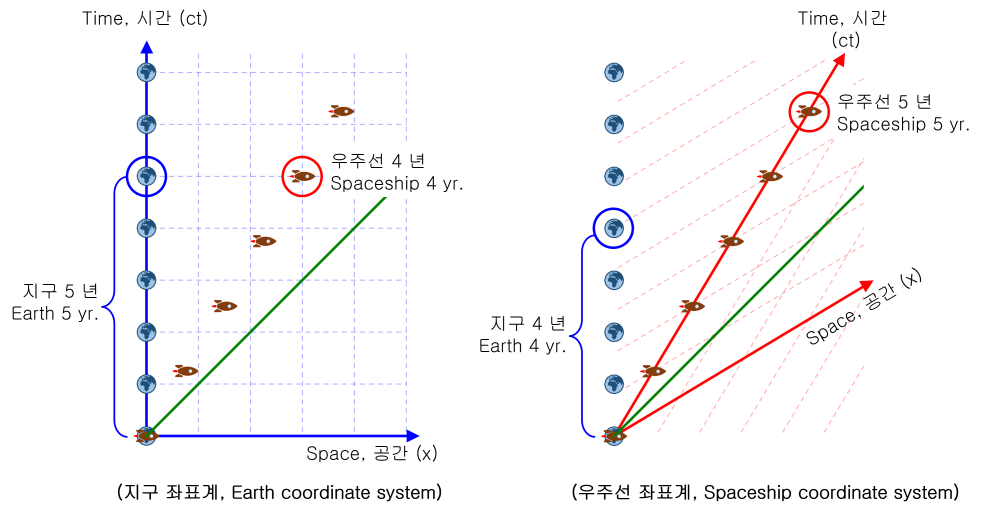
上の図は、宇宙船が光束の0.6倍で地球から離れることを示しています。 2つの図は互いに同じ動きであり、座標系だけが異なるように観察されたものです。
地球中心座標系で見ると、宇宙船の時間がゆっくりと流れています。
ところで、宇宙船中心座標系で見ると、地球の時間がゆっくりと流れているようです。
これは、それぞれの座標系で相手を観察するためです。
宇宙船が方向を変える場合
宇宙船が地球に戻るためには方向を変えなければならず、方向を変える過程で減速と加速が行われます。 この過程でミンコフスキー時空間の軸が以下のように変形します。 (赤→オレンジ色)
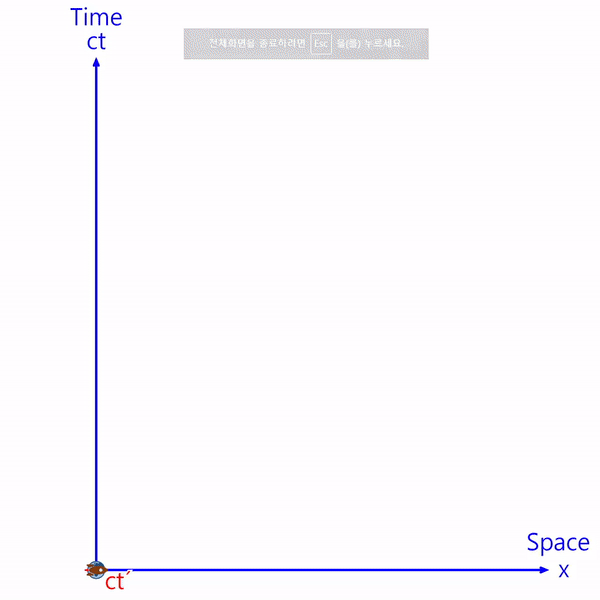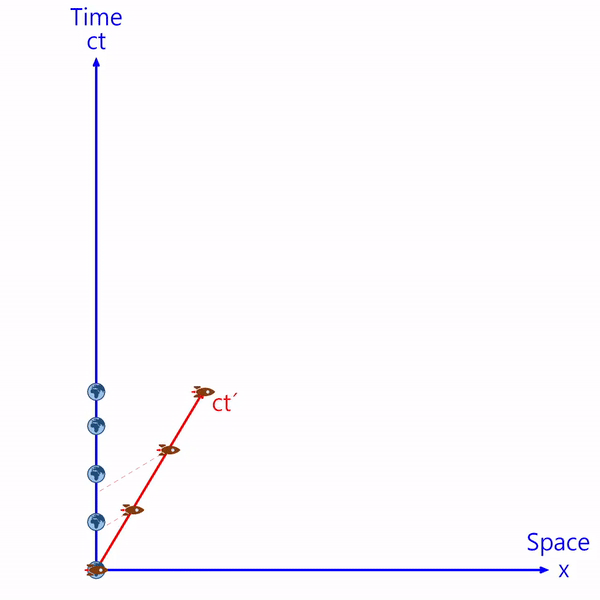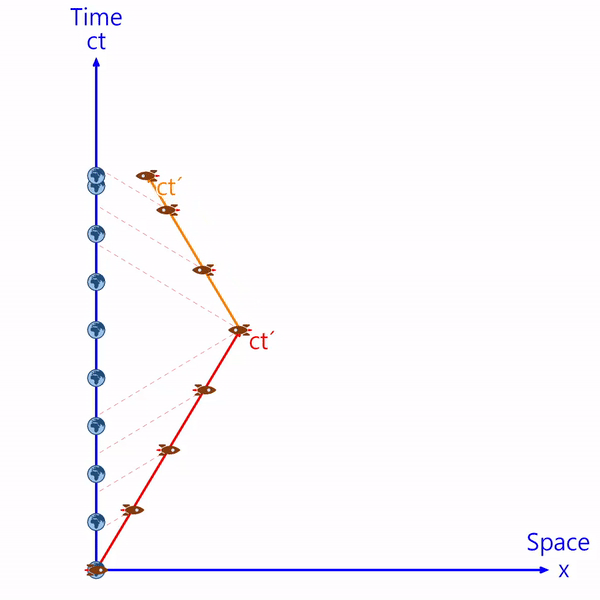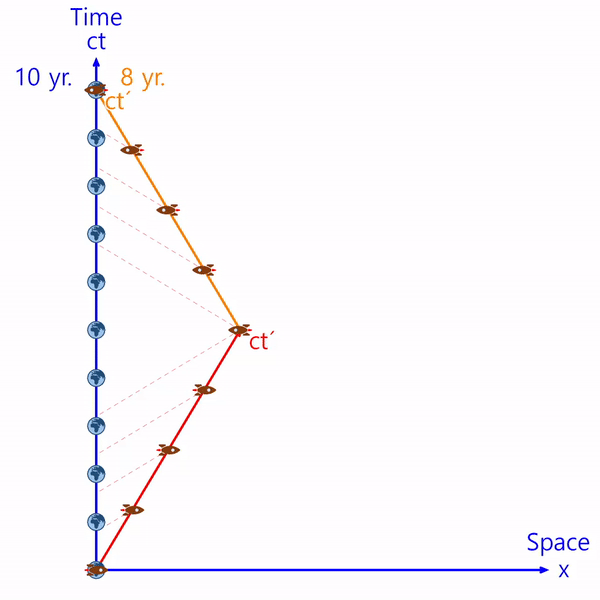
点線は宇宙船座標系のx軸です。 (宇宙船と同じ時間帯)
宇宙人の立場では速度だけが変わったようですが、実際には座標系の軸が変わるので地球では数年の時間がジャンプされてしまいます。
事実、途方もない減速と加速を行う過程で、宇宙船はブラックホールの近くにあるように大きな重力加速度を経験しなければなりません。 そして、この間宇宙船の外の時間が多く流れてしまいます。