注意:動く物体の長さが収縮しているように見える結果を導き出すには、このシミュレーションの説明を最後まで読んでください。 (特殊相対性理論を上記のシミュレーションだけで説明するのは難しい。)
このシミュレーションで使用される記号の意味は次のとおりです。
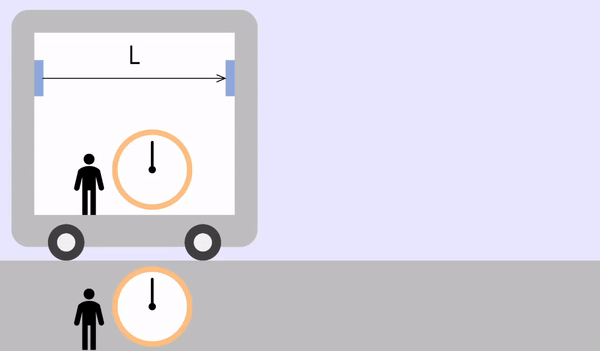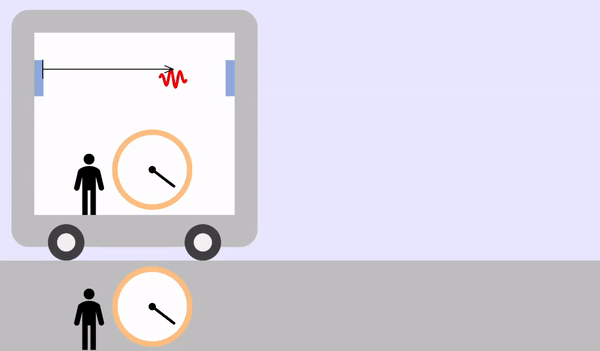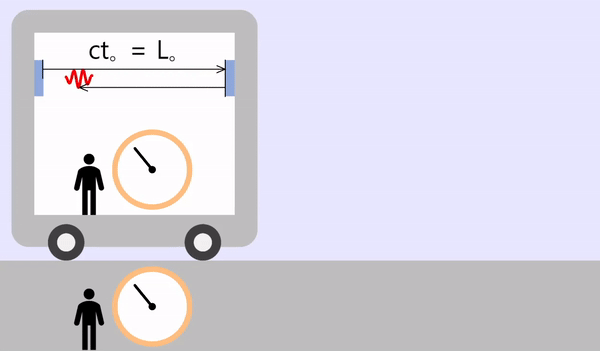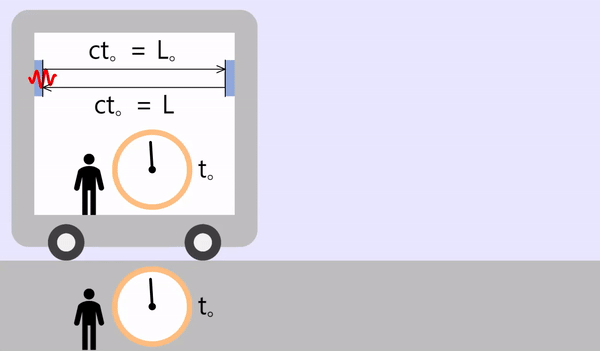
- L。 = 車が停止している間に光が移動した距離(「距離=速さ × 時間」なので「ct。」と同じ)
- c = 光の速さ (≒ 299,792,458 m/s)
- t。 = 車の内部で観察された光の移動時間(または静止状態で観察した光の移動時間)
- t = 車の外から観察した光の移動時間
- v = 車の速さ
特殊相対性理論
特殊相対性理論は、光の速さなど、非常に速く移動する物体を扱う物理理論です。 物体の速度が増加すると、古典力学(ニュートン力学)では説明できない現象が現れます。これを説明するための理論は特殊相対性理論であり、古典力学と完全に互換性があります。
特殊相対性理論は、誰もが知っている有名な物理学者、アルバート・アインシュタインのアイデアです。
仮定
特殊相対性理論は、次の2つの仮定から始まります。
- どちらの慣性系でも、物理法則は等しく適用されます。
「慣性計」とは、一定の速さで走る列車のように速さの変化がない空間をいいます。
列車の外で適用される物理法則(慣性の法則、F = ma、作用・反作用、(各)運動量およびエネルギー保存の法則)は、列車の中でも等しく適用されます。実際、列車は停止しており、移動するのは列車外の風景だと仮定しても、これを区別する方法はありません。 - どの慣性計で観測しても、光の速さは同じように観測されます。
非常に早く動く宇宙船からどんな光が放出されたと考えてみましょう。宇宙船で観測された光の速さが\(c\)であり、宇宙船の速さが\(u\)であれば、外部から観測した光の速さは\(u+c\)と思われるが、光の速さは依然として\ (c\) になります。この光は、ある慣性計の別の観察者が観測しても、まだ\(c\)です。
特殊相対性理論によって起こること
特殊相対性理論によると、次のような面白いことが起こります。
- 時間(時刻の隔たり)の伸び:速く動く慣性計は、時間がゆっくりと流れるように観測されます。
- ローレンツ収縮: 速く動く慣性計は、移動する方向軸の長さが短くなるように観察される。
時間の伸び(時刻の隔たり)
時間の伸びの説明については、下記のリンクをご覧ください。
ローレンツ収縮
非常に速く移動している物体は、長さが収縮していると測定されます。
例えば、列車の左側から光が放出され、右鏡に反射されてから、戻ってくる場合を考えてみましょう。
列車が停止している場合(または列車内)
列車の内側と外側が同じ慣性計です。
光の往復にかかる時間は次のとおりです。(\(t_o\) = 停止状態の時間、\(L_o\) = 停止状態の間隔)
\[t_o = \frac{2L_o}{c}\]
列車が速さ\(v\)に移動する場合
出発した光が右に移動するのにかかる時間を \(t_1\) とすると、移動距離は \(L + vt_1\) です。 光の立場での移動距離は \(ct_1\) で、2 つの値はお互いに同じです。
\[L + vt_1 = ct_1\\ \color{red}{\therefore t_1 = \frac{L}{c-v}}\]
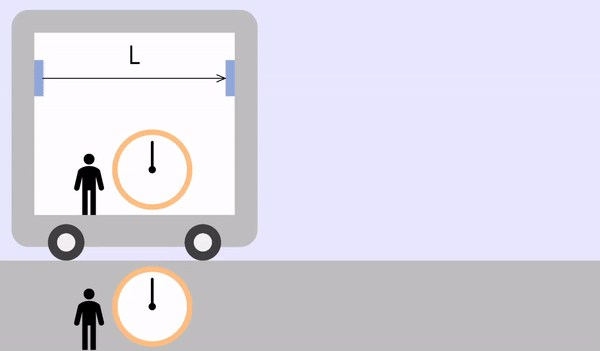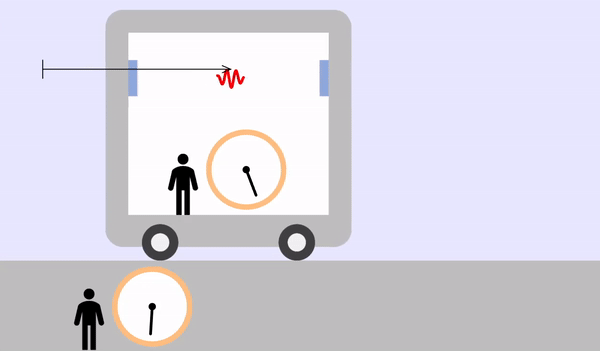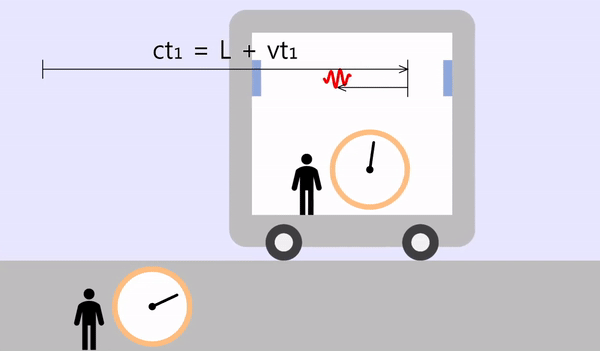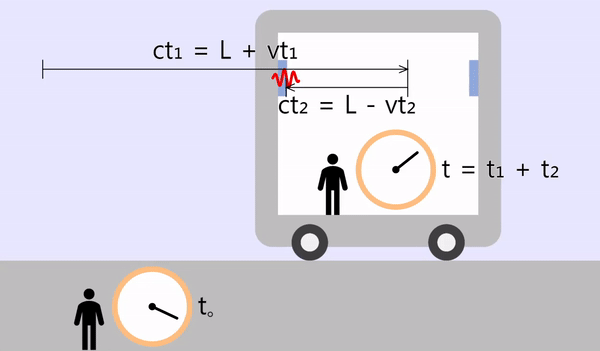
反射光が左に移動するのにかかる時間を \(t_2\) とすると、移動距離は \(L - vt_2\) です。 光の立場での移動距離は\(ct_2\)であり、2つの値はお互いに同じです。
\[L - vt_2 = ct_2\\ \color{red}{\therefore t_2 = \frac{L}{c+v}}\]
光が戻ってくるのにかかる合計時間は、\(t_1\)と\(t_2\)の合計になります。
\[t = \color{red}{t_1} + \color{red}{t_2} = \frac{L}{c-v} + \frac{L}{c+v} = \frac{2Lc}{c^2 - v^2}\]
往復にかかる時間 \(t\) を時間膨張方程式 \(t = \frac{t_o}{\sqrt{1-\frac{v^2}{c^2}}}\) の時間 \(t\ )と同じだとすると、
\[L = L_O \sqrt{1 - \frac{v^2}{c^2}}\]
言い換えれば、移動する物体の長さは常に短くなるように測定される。
そして、同じ物体でも誰が測定するかによって異なる値で測定されます。