RLC直列回路

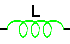
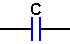
抵抗(R) - インダクタ(L) - コンデンサ(C)が直列に接続された回路を考えてみましょう。
毎瞬間回路に流れる電流は、回路のどの点でも同じです。 (非常に重要だから、ぜひ覚えておきましょう。)
電流は全体的に一定であるが、それぞれの部品にかかった電圧の高さはそれぞれ異なります。
インダクタに形成される電圧は、逆起電力によるものです。交流正弦波では、電流の変化が最も急な点で逆起電力は、すでに最大値になります。したがってインダクタに誘導される逆起電力は、電流より90˚位相が先に行きます。
コンデンサは、インダクタと少し異なります。コンデンサに形成される電圧は、コンデンサに電荷がたまって形成されることです。交流正弦波では、コンデンサに最大で電荷が多くたまっているときは、電流の方向が変わる直前になります。したがって、コンデンサの電圧は電流より90˚位相が遅れています。
インダクタとコンデンサが直列に接続された場合には、インダクタに誘導される電圧とコンデンサに溜まった電荷に生じた電圧は、互いに180˚位相を示します。
共振周波数
「インダクタの誘導リアクタンス(直流回路の抵抗のような役割)」と 「コンデンサの容量リアクタンス(直流回路の抵抗のような役割)」は、電圧と同様に相互に位相が180˚逆になります。
インダクタとコンデンサが直列に接続された回路の場合、交流のインピーダンス(Impedance)は、単に合計するのではなく、位相関係を計算してベクトルの合算方法で計算する必要があります。
交流回路での抵抗の役割をするインピーダンスは、
\[ Z=\sqrt { { R }^{ 2 }+{ ({ X }_{ L }-{ X }_{ C }) }^{ 2 } } \]
になります。
インピーダンスは、「リアクタンス差(XL - XC)」と「一般抵抗値(R)」をそれぞれ底辺と高さとする直角三角形の斜辺の長さと同じです。
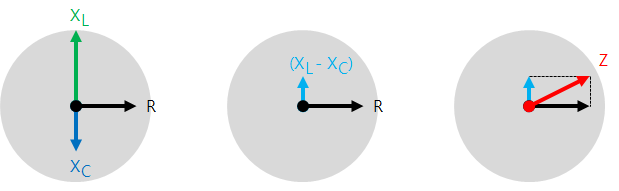
インダクタとコンデンサの位相が互いに反対であるので、交流電源の周波数をうまく調節すれば、回路に流れる抵抗が最も小さくすることができます。つまり、誘導リアクタンスと容量リアクタンスサイズを同じにして、互いに相殺させます。
\[ X_L = X_C \]
であれば、されるので、
\[ 2\pi fL=\frac { 1 }{ 2\pi fC } \]
\[ f=\frac { 1 }{ 2\pi \sqrt { LC } } \]
がされるが、この周波数を共振周波数(固有周波数)とします。
この場合、誘導リアクタンスと容量リアクタンスが相殺されてたので、回路の電流は、唯一の抵抗による効果のみです。
交流は、周波数に応じて誘導リアクタンスと容量リアクタンスが異なりますので、電流値も周波数によって異なります。
つまり、RLC回路を用いて、所望の周波数の電流のみ選ぶことができます。
この方法は、ラジオや無線通信回路に広く使用されます。
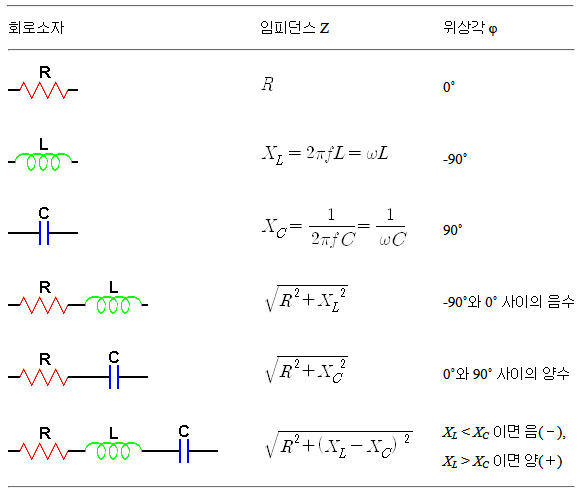
様々な回路素子の照合からなる直列回路のインピーダンス値と位相角