砲弾が人工衛星になるには
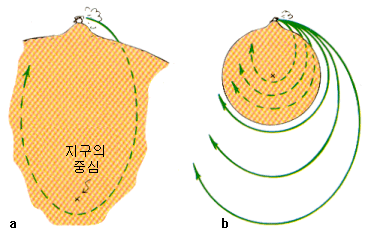
a. 砲弾が放物線を描いて落下すると考えてみましょう。砲弾が描く軌跡は、実際に地球の中心を焦点とする楕円軌道の一部です。地球の中心は、楕円の遠い焦点に対応します。
b. 砲弾が地表面と衝突しない場合は、少なくとも8km/s(正確に、7920m/s)の速度で地表面と水平に発射されます。速度がこれより速くなると、地球の中心点を楕円の近くに焦点とする楕円運動をします。
スーパーマンが投げた人工衛星
スーパーマンが高い山の上に石を投げるとするとき、どのような速度で投げるかによって、さまざまな運動をします。
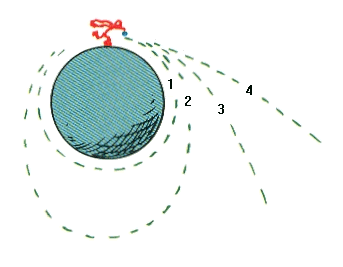
- ≒ 8km/s
地球の表面の曲率と一致して、円形の軌道を回ります。ただし、地球の屈曲にぶつけたり大氣との摩擦がないと仮定の下でのみ可能です。投げられた衛星は、約90分後に地球を一周回って元の位置に戻ります。 - < 11.2km/s
楕円軌道を回って、戻ってくるには、90分以上かかります。 - ≒ 11.2km/s
双曲線軌道を描きます。これより速いスピードで投げたら、ボールは戻ってきません。 - > 11.2km/s
地球を脱出することができます。 - > 42.5km/s
太陽系を脱出することができます。
求心力、人工衛星が回転するようにする力
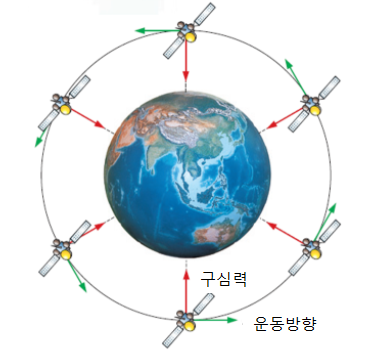
目にはよく見えませんが、現在、地球上には数多くの人工衛星が回っているが、この衛星は地球の周りの一定の軌道に等速円運動をしています。地球の重力がまさに求心力になります。
円軌道を維持するための速度の計算
半径が「r」である円形の軌道を回っている人工衛星について考えてみましょう。
重力と求心力が同じだと考えると、衛星は円運動をするようになります。
\[ \begin{align} ( 求心力 &= 重力 ) \\ m\frac { { v }^{ 2 } }{ r } &=G\frac { Mm }{ { r }^{ 2 } } \end{align} \]
脱出速度の計算
人工衛星に作用する位置エネルギーを人工衛星の運動エネルギーに補償があれば、地球からの脱出が可能になります。
\[ \begin{align} ( 人工衛星の\\運動エネルギー &= 位置エネルギー ) \\ \frac { 1 }{ 2 } m{ v }^{ 2 }&=G\frac { Mm }{ r } \end{align} \]
落ちている月
リンゴを木から剥離する力と同じ種類の力が月にも作用します。
月は地球の重力のために、1秒間1.4mm落下します。
