パスカルの三角形
パスカルの三角形は、数学で二項係数(異なるいくつかのものの中からランダムに物事を選択した場合の数)を三角形状の幾何学的形状に配列したものです。
これは、パスカルで名前が付けられたが、すでに数世紀前に、他の人からの研究されたものです。
パスカルの三角形は、その中に数学的に興味のある現象がたくさん隠れています。
パスカルの三角形を作り方
上部の両側斜め方向から譲り受けた数字を互いに加えるとパスカルの三角形が作られます。
三角形の両側斜面の数は「1」にします。
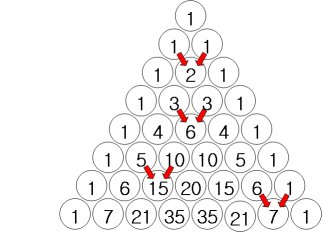
パスカルの三角形の特徴
- 各行の合計は、2の累乗のとおりです。
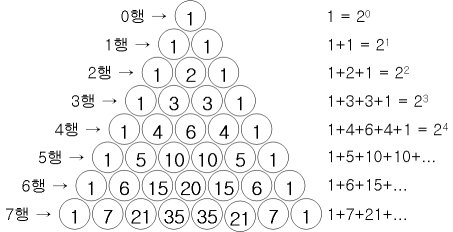
- 数字の意味=上部数列の和となります。
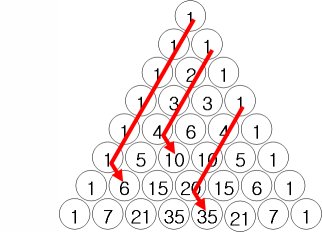
- 各列リストされことは、特別な意味を持ちます。
第1列 = すべての自然数「1」です。
第2列 = 自然数の数列
第3列 = 三角数(モノを集めて正三角形状にすることができるものの数)
第4列 = 三角錐数(モノを積ん正四面体の形に作ることができるものの数)

- フィボナッチ数列になります。
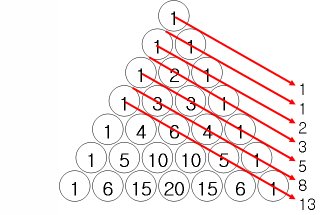
- 0行の数列 = 0つのものの中からレンドプで物事を選択する組み合わせの種類の数
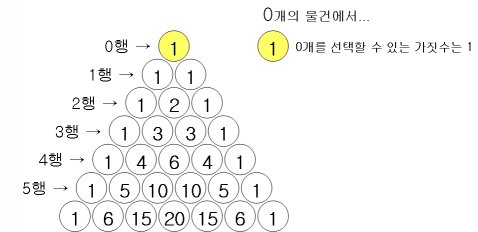
- 1行の数列 = 1つのものの中からレンドプで物事を選択する組み合わせの種類の数
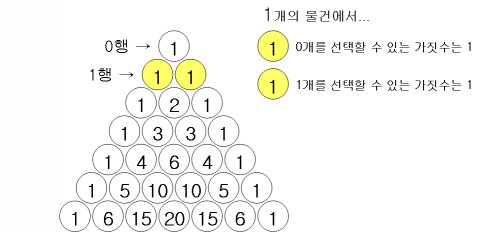
- 2行の数列 = 2つのもの(A, B)の中からレンドプで物事を選択する組み合わせの種類の数
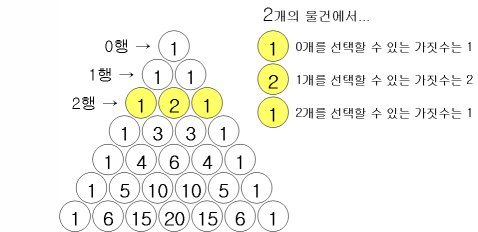
- 2行の数列 = 2つのもの(A, B, C, D)の中からレンドプで物事を選択する組み合わせの種類の数
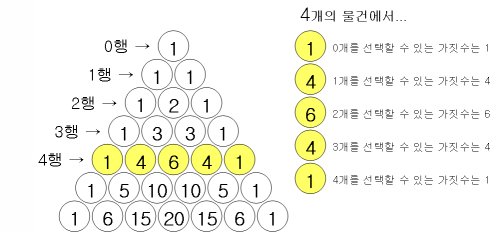
シェルピンスキーの三角形 Sierpinski Curve

2の倍数に該当する数字を着色してみると、同じ形が繰り返されます。
形をよく見ると、部分と全体がお互いに似ています。部分の姿が繰り返されて、全体の姿になるということは、フラクタルの基本原理に対応します。
- 3の倍数に該当する数字を着色した場合

- 4の倍数に該当する数字を着色した場合
