交流電流は、インダクタ(コイル、Inductor)が細かくすればするほど通過することは困難です。
 インダクタ(コイル)は、導線を巻いて作った部品です。
インダクタ(コイル)は、導線を巻いて作った部品です。
直流電流を流す場合に、インダクタは、純粋な線でのみ動作します。
このインダクタに交流電圧をかけてくれれば、インダクタは、まるで抵抗のように動作します。
インダクタに流れる電流が変化する、その変化を妨げる逆起電力が生じて電流の流れを妨げます。
インダクタガ抵抗のように行動する性質は、インダクタの「自己インダクタンス(L)」が大きいほど、そして交流の「周波数(f)」が高いほど大きくなります。
周波数「ω」の交流電圧「V」は、独自のインダクタンス「L」であるインダクタに加わると、電流「I」は、
\[I\quad =\quad \frac { V }{ \omega L } \quad =\quad \frac { V }{ 2\pi fL } \]
です。
このとき、直流回路の抵抗のような役割をする 「 \( 2\pi fL \)」 をインダクタの「誘導リアクタンス(inductive reactance)」と呼ばれます。
そして、簡単に「XL 」で表し、単位は「Ω」を使用します。
\[{ X }_{ L }\quad =\quad 2\pi fL\quad =\quad \omega L\]
直流電流で電気抵抗は、電流の流れを妨げると同時に、消費電力を発生させます。しかし、インダクタは、電流の流れを妨げるが、消費電力を発生させません。
これは、インダクタの電圧と電流の方向が同じ方向であるときは、電源から供給されるエネルギーは、インダクタに磁界のエネルギーとして保存され、電圧と電流の方向が逆になると、そのエネルギーを戻してくれるからです。
さて、それ自体誘導現象による逆起電力のために、電流の位相は電圧(インダクタ端子間電圧)よりも遅れています。
交流電流は、コンデンサー(キャパシタ、Capacitor)をスキップして進むことができます。
 コンデンサは、基本的に導線の一部が切断されたのと同じです。
コンデンサは、基本的に導線の一部が切断されたのと同じです。
したがって、直流電流は、コンデンサをスキップ進めることができません。
しかし、交流電源にコンデンサを接続すると、電流が継続流れます。これは、電流の方向が周期的に変わり、コンデンサの両方の極での充電と放電が繰り返されて、電流が流れる効果が起こるからです。
コンデンサを交流電源に接続したとき、コンデンサの電気容量が大きいほど、交流の周波数が高いほど多くの電流が流れます。
電気容量が「C」であるコンデンサに交流電圧「V」をかけて与えるとき、回路に流れる電流の強さ「I」は、
\[I\quad =\quad \frac { V }{ \left( \frac { 1 }{ \omega C } \right) } \quad =\quad \frac { V }{ \left( \frac { 1 }{ 2\pi fC } \right) } \]
です。
このとき、直流回路の抵抗のような役割をする 「 \( \frac { 1 }{ 2\pi fC } \) 」 を「容量リアクタンス(capacitive reactance)」と呼ばれます。
そして、簡単に「XC 」で表し、単位は「Ω」を使用します。
\[{ X }_{ C }\quad =\quad \frac { 1 }{ 2\pi fC } \quad =\quad \frac { 1 }{ \omega C } \]
コンデンサは、交流回路での抵抗の役割をするが、消費電力は「0」です。
交流回路に接続されたコンデンサは、電流が増加するときには、エネルギーを保存し、電流が減少するときは、保存されたエネルギーをすべて戻してくれるので、エネルギーを消費しません。
コンデンサに充電された電荷が一つもない場合かかった電圧が「0」であり、このときの電流は、最大値を持ちます。
従って、電圧(コンデンサ端子間電圧)の位相が電流の位相よりも遅れています。
インピーダンスとは交流回路の合成抵抗をいいます。

 交流の「インピーダンス(Impedance)」は、単に合計するのではなく、位相関係を計算してベクトルの合算方法で計算する必要があります。
交流の「インピーダンス(Impedance)」は、単に合計するのではなく、位相関係を計算してベクトルの合算方法で計算する必要があります。
交流回路での抵抗の役割をするインピーダンスは、
\[Z\quad =\quad \sqrt { { R }^{ 2 }+{ ({ X }_{ L }-{ X }_{ C }) }^{ 2 } } \]
になります。
交流回路の抵抗値が最も小さいために、
\[ { X }_{ L } = { X }_{ C } \]
であれば、されるので、
\[ \begin{align} 2\pi fL &= \frac { 1 }{ 2\pi fC } \\ f &= \frac { 1 }{ 2\pi \sqrt { LC } } \end{align} \]
がされるが、この周波数を共振周波数(固有周波数)とします。
交流は、周波数に応じて「誘導リアクタンス」と「容量リアクタンス」が異なりますので、電流値も周波数に依存します。
RLC回路を用いて、所望の周波数の電流のみ選ぶ方法は、ラジオや無線通信回路に広く使用されます。
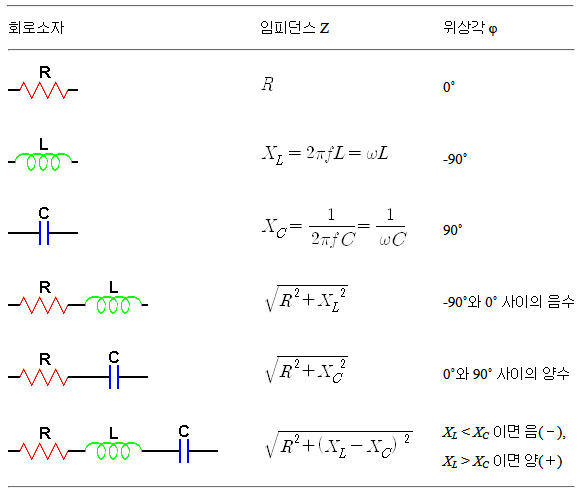
様々な回路素子の照合からなる直列回路のインピーダンス値と位相角