電池と負荷
電気回路の電池は、電圧差を維持して回路に電流が流れるようにします。
電池が維持させる電圧差によって電流が流れ、エネルギーを消費することになるが、エネルギーが消費されるところを負荷と呼びます。普通学校の研究室での負荷は小さい電球や抵抗になります。
すべての電気回路からの電圧は、上昇しただけ下がります。上がった高さと下がった高さを数値で表すことができている場合上がった高さと下がった高さの合計は、「0」になります。これは遊園地のジェットコースターを考えると簡単です。ジェットコースターに乗って、最初は高い所に上がります。その次のジェットコースターは、下にずっと降りながらぴりっとを楽しむされます。ロールコースターが途中で上り下りしても下がった全体の高さは上がった全体の高さと同じです。
抵抗の直列接続
抵抗2個を直列接続した場合、抵抗は、それぞれの電圧を分割持っ店になります。この場合、それぞれの抵抗にかかる電圧は、元の電圧よりも小さくなります。二つの抵抗にかかる電圧を、すべてのよりしなければなら元の電圧になります。
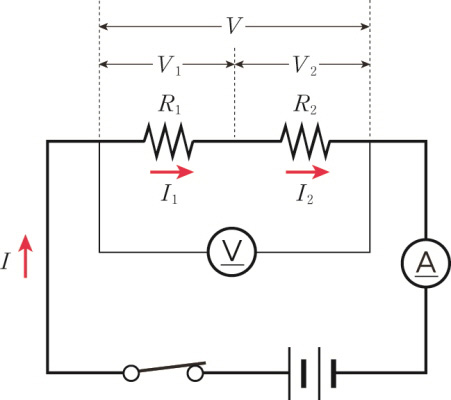
2つの抵抗が直列に接続されているときに、それぞれの抵抗に流れる電流は、回路全体に流れる電流の強さと同じです。
\[ I\; =\; { I }_{ 1 } \; = \; { I }_{ 2 } \]
さて、回路にかけてくれたすべての電圧「V」は、二つの抵抗に分かれてかかりますので、それぞれの抵抗にかかる電圧の合計は、全体の電圧になります。
\[ V\; =\; { V }_{ 1 }+{ V }_{ 2 } \]
回路全体に流れる電流の強さを「I」とすると、オームの法則から、 「V1 =IR1, V2 =IR2」 になります。
回路の合成抵抗を「R」といえば、オームの法則から「V = IR」であるため、次のような関係が成立します。
\[ V\; =\; { V }_{ 1 }+V_{ 2 }\; =\; I{ R }_{ 1 }+I{ R }_{ 2 }\; =\; I({ R }_{ 1 }+{ R }_{ 2 }) \]
\[ \therefore \; R\; =\; { R }_{ 1 }+{ R }_{ 2 } \]
つまり、二つの抵抗が直列に接続されているときに、合成抵抗は、それぞれの抵抗を加えたものです。したがって抵抗を直列に接続すると、合成抵抗が大きくなります。
抵抗の並列接続
抵抗2個を並列接続した場合には、それぞれの抵抗にかかる電圧は、元の電圧と同じです。並列接続された抵抗は、その数に関係なく、元の電圧と同じです。
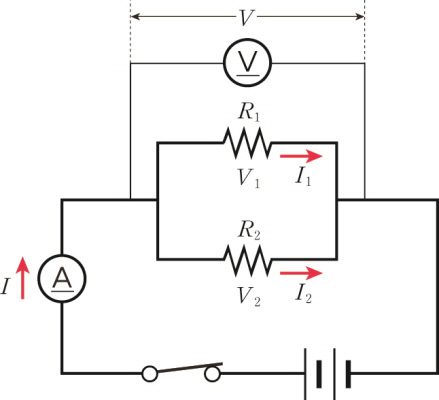
抵抗が並列に接続されているときに、それぞれの抵抗に流れる電流を加えると全体の回路に流れる電流の強さと同じです。
\[ I\; =\; { I }_{ 1 }+{ I }_{ 2 } \]
さて、抵抗が他の抵抗を通過せずに直接電源に接続されているので、それぞれの抵抗にかかる電圧は、全体の電圧と同じです。
\[ V\; =\; { V }_{ 1 } \; = \;V_{ 2 } \]
回路にかかる電圧を「V」とすると、オームの法則から、 「I1 = V / R1, I2 = V / R2」 になります。
回路の合成抵抗を「R」といえば、オームの法則から「V = IR」であるため、次のような関係が成立します。
\[ I\; =\; { I }_{ 1 }+{ I }_{ 2 }\; =\; \frac { V }{ { R }_{ 1 } } +\frac { V }{ { R }_{ 2 } } \; =\; V(\frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } ) \]
\[ \therefore \; \frac { 1 }{ R } \;=\; \frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } \]
つまり、二つの抵抗が並列に接続されているときに、合成抵抗の逆数は、それぞれの抵抗の逆数をすべて加えたものです。したがって、抵抗を並列に接続すればするほど、合成抵抗は小さくなります。