重力は、
質量があるすべての物体の間に引きつける力です。
ニュートン(Newton)によると、質量を持った二つの物体がお互いを引きつける力は、二つの物体の質量の積に比例し、二つの物体間の距離の二乗に反比例します。
 \[F=G\frac { { m }_{ 1 }{ m }_{ 2 } }{ { r }^{ 2 } } \]
\[F=G\frac { { m }_{ 1 }{ m }_{ 2 } }{ { r }^{ 2 } } \]
ここで、「m1」と「m2」は質量(kg)であり、「r」は、二つの質量中心間の距離(m)、「G」は、ニュートン定数と呼ばれる比例定数です。計算された力の単位は、「ニュートン(N)」です。
上式によれば、質量「m1」と「m2」が大きければ大きいほど、重力は大きくなります。そして、二つの物体間の距離が大きくなればなるほど、重力はそれらの質量中心間の距離の二乗に反比例して弱くなります。つまり、距離が2倍、3倍、4倍離れると重力は1/4倍、1/9倍、1/16倍弱くなります。
ニュートンが発見した重力の法則は非常に素晴らしいし、小さなリンゴから太陽系はもちろん、千億個の星を従えた巨大な銀河の衝突も説明することができました。ニュートン以来の古典力学の新しい復興期を迎えたといっても過言ではありません。
重力定数「G」を調べる
重力を計算する式で、「G」は、特に定められた数字です。
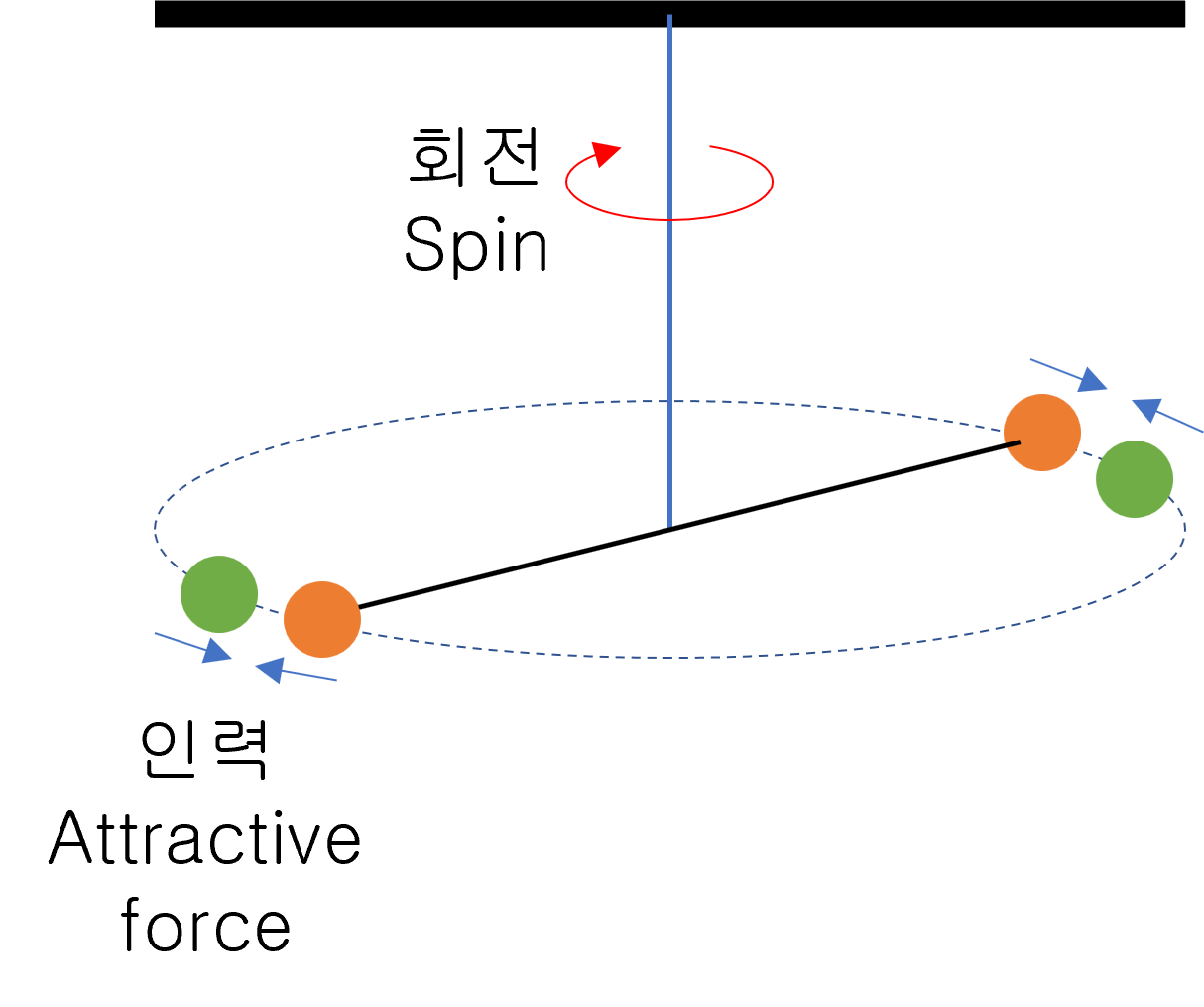
この数字は、Henry Cavendishが非常に精密な実験で測定しました。
「G」を測定するためには、Cavendishはねじり秤を使用しました。ねじり秤は非常に敏感で小さな力でも回転をします。
このとき、ねじれ角とスケールの特性であるねじり定数さえ分かれば、両者の間の重力を測定することができます。
正確な実験の結果、「G」の値は、
です。
「G」の値は非常に小さい方です。つまり、重力を電磁力と比較すると、重力は非常に小さな値を持ちます。たとえば、(+)の電気を帯びた陽子と( – )の電気を帯びた電子が互いに引き寄せる電気力は重力に比べて1039倍強いです。
電気力が重力に比べてとても強いが、実際の天体は、主に重力によって移動します。
重力は引力だけ存在するが、電磁力は、押したり引いたりの力がお互いを相殺してしまう効果を出すためです。