물리학에서의 적분

정적분

2차원 좌표평면에서 정적분은 그래프의 면적을 구하는 방법입니다.

면적을 가로와 세로 길이의 곱으로 간단하게 구할 수 있는 경우는 오직 직사각형의 경우입니다.
모양이 일정하지 않으면 단순 곱셈으로 면적을 구할 수 없습니다. 그래프의 어떠한 구간이 정해져 있을 때, 우리는 그 구간의 면적을 구하기 위해 정적분을 이용합니다.

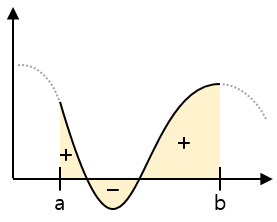
정적분의 수학적인 정의는 다음과 같습니다.

구간의 폭이 한없이 작게 되도록 구간을 분할할 때 이 합이 항상 일정한 값에 한없이 가까워지게 되면, 그 값을 f(x)의 a부터 b까지의 정적분으로 정의합니다.
\[ (면적) =\, \int_{a}^{b} f(x) \; dx \]

정적분하는 방법

적분을 하기 위해서는 우선 미분을 알아야 합니다.
미분법에 대해서는 각자 검색해 보기 바랍니다.

적분은 미분의 역함수라고 말할 수 있습니다. 어떤 함수 F(x)를 x에 대해 미분한 함수를 f(x)라고 가정합시다. 이 경우, f(x)를 적분하면 F(x) + C(적분상수)가 됩니다.
적분 과정이야 어떻게 되었든 간에, 함수식을 적분할 수 있다면, 정적분 값은 다음과 같이 구할 수 있습니다.

\[ \int_{a}^{b} f(x) \; dx \, = \, F(b) – F(a) \]

물리학에서 자주 사용되는 정적분의 사례

속력-시간 그래프		면적 = 구간의 시간 동안 이동한 거리
가속도-시간 그래프		면적 = 구간의 시간 동안 속력이 변화한 정도
힘-시간 그래프		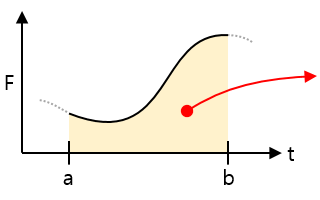면적 = 구간의 시간 동안 받은 충격량(운동량)
힘-거리 그래프		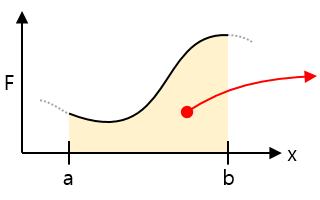면적 = 구간의 거리를 이동하는 데 한 일의 양, 용수철인 경우 용수철에 저장되거나 풀려나온 에너지