* 위 시뮬레이션의 기체 분자들은 모두 같은 종류이며, 분자의 색은 단지 식별을 위한 것입니다.
기체 분자 운동론
기체 분자 운동론은 기체 분자의 운동을 설명하기 위한 가설입니다. 이 가설을 설명하기 위해 다음과 같은 가정을 만족시키는 이상 기체를 가정합니다. (위키백과)
- 기체 분자는 질량은 존재하지만, 부피는 존재하지 않는다.
- 기체 분자는 공간을 통해 힘을 교환하지 않습니다.
- 기체 분자가 일으키는 모든 충돌은 완전 탄성 충돌이다.
- 기체는 어떤 온도나 압력에도 절대로 액화 또는 승화되지 않는다.
- 기체 분자의 평균 분자 운동 에너지는 절대 온도에만 비례하며, 분자의 크기, 모양 및 종류에는 영향을 받지 않는다.
기체 분자의 근평균제곱속력
벽면의 단면적이 \(A\)이고, 길이가 \(L\)인 상자 속에 질량이 \(m\)인 기체 입자가 들어 있습니다.
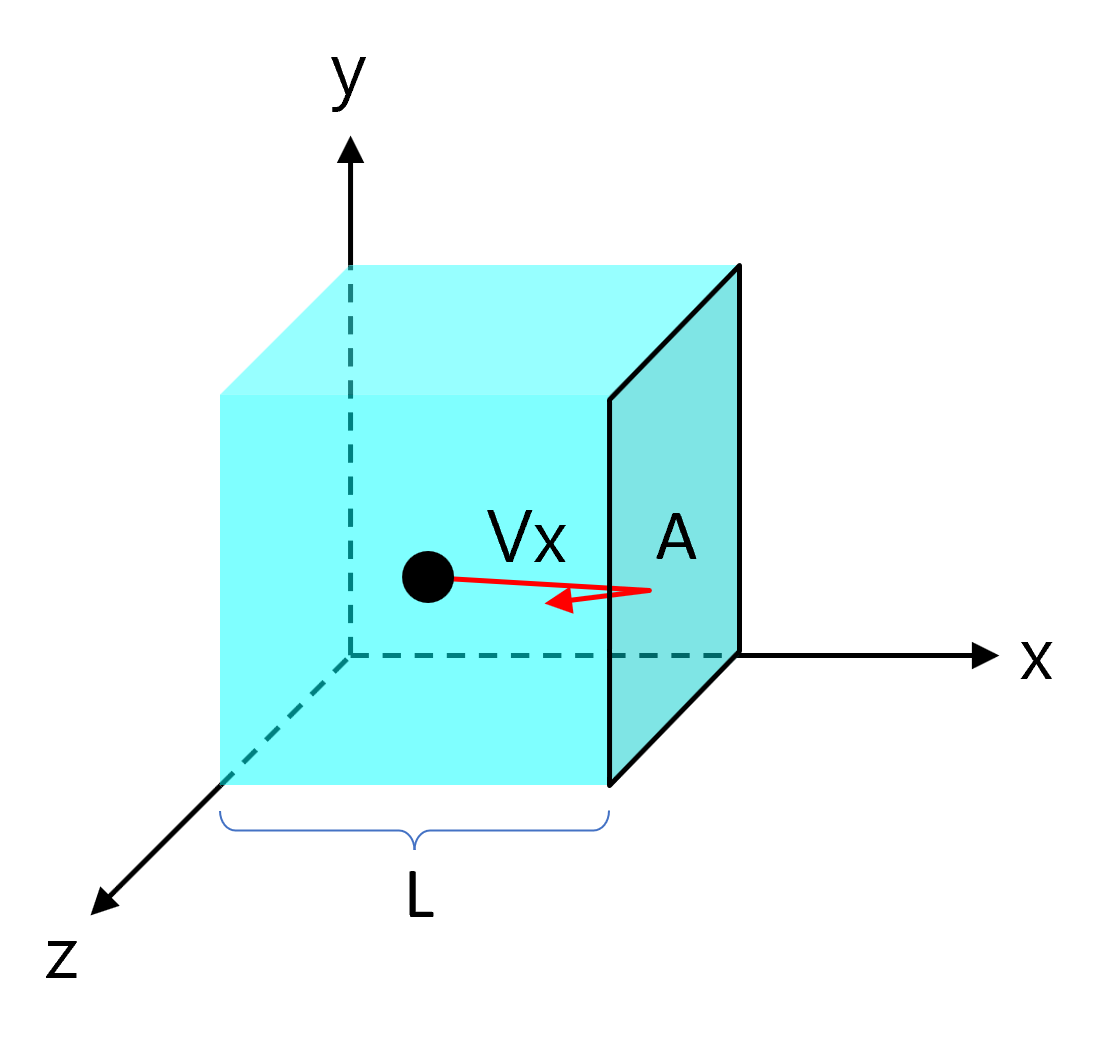
기체 입자는 벽면과 완전 탄성 충돌을 하며, \(x\), \(y\), \(z\)축 방향으로 무질서한 직선 운동을 하고 있습니다.
기체 입자가 \(v_x\)의 속도를 가지고 상자의 \(A\)면과 충돌하는 경우를 생각해 봅시다. 벽면 \(A\)에 충격을 가하는 운동은 \(x\)축 성분 뿐이므로, 편의를 위해 당분간 \(y\)축과 \(z\)축은 생각하지 않습니다.
기체 입자는 벽면 \(A\)와 완전 탄성 충돌을 합니다. 충돌 전 후 입자의 운동량은 다음과 같이 변합니다.
\[ \Delta P_x = mv_x – (-mv_x) = 2mv_x \]
기체 분자가 면적 \(A\)인 상자의 한쪽 벽면과 충돌을 일으킨 뒤, 반대쪽 벽면과 충돌하고, 다시 \(A\)면을 충돌하는데 걸리는 시간은 다음과 같습니다.
\[ \Delta t = \frac{2L}{v_x} \]
기체 분자가 매초당 벽면 \(A\)에 가하는 충격력 \(F\)는 운동량의 변화량을 시간으로 나누어서 구할 수 있습니다.
\[ F = \frac {\Delta p}{\Delta t} = \frac {2mv_x}{\frac{2L}{v_x}} = \frac{mv_{x}^{2}}{L} \]
벽면 \(A\)에 가해지는 압력 \(P\)는 단위 면적당 힘으로 정의되므로, 기체의 압력은 다음과 같습니다. (부피 \( V = AL\))
\[ P = \frac{F}{A} = \frac{\frac{mv_x^2}{L}}{A} = \frac{mv_x^2}{AL} = \frac{mv_x^2}{V} \]
기체 분자가 2개 이상인 경우, 기체 분자들이 벽면 \(A\)에 가하는 압력 \(P\)의 크기는 다음과 같습니다.
\[ \begin{align} P &= \frac{mv_{x1}^2}{V} + \frac{mv_{x2}^2}{V} + \frac{mv_{x3}^2}{V} \cdots\\ &= \frac{m(v_{x1}^2 + v_{x2}^2 + v_{x3}^2 \cdots )}{V} \\ &= \frac{mN \overline{v_x^2}}{V} \end{align} \]
\(N\) = 기체 분자의 개수
\(\overline{v_x^2}\) = 입자의 \(x\)축 방향 속도 제곱의 평균값
파스칼의 원리에 따라서, 기체의 압력은 모든 벽면에 걸쳐 균일하게 적용됩니다.
따라서, 위에서 구한 압력 \(P\)는 단순히 벽면 \(A\)에만 해당되는 것이 아니라, 상자 전체 벽면에 동일하게 적용됩니다.
이제, \(y\)축과 \(z\)축 방향을 고려해 보겠습니다. 기체 입자의 속도 제곱(\(v_{rms}^{2}\))의 평균은 피타고라스의 정리로 나타낼 수 있습니다.
\[ \overline{v_{rms}^2} = \overline{v_x^2} + \overline{v_y^2} + \overline{v_z^2} \]
이상 기체 분자의 운동에서는 모든 축에서 같은 자유도를 가지기 때문에, 다음과 같이 간단하게 생각할 수 있습니다.
\[ \overline{v_{rms}^2} = 3\overline{v_x^2} \\
\therefore \overline{v_x^2} = \frac{1}{3}\overline{v_{rms}^2} \]
따라서, 상자 전체에 가해지는 압력은 다음과 같습니다.
\[ P = \frac{1}{3} \frac{mNv_{rms}^2}{V} \]
기체 입자의 전체 질량 \(mN\)은 \(nM\)(=몰수(\(n\))×몰질량(\(M\)))으로도 나타낼 수 있습니다.
\[ P = \frac{1}{3} \frac{nMv_{rms}^2}{V} \\ \therefore PV = \frac{1}{3} nMv_{rms}^2 \]
위의 결과는 이상기체 상태방정식(\(PV=nRT\))과도 일치해야 합니다.
\[ (PV=\,)\:\:\:\: \frac{1}{3} nMv_{rms}^2 = nRT \]
위 등식으로부터 평균제곱속력(\(v_{rms}^2\))은 절대 온도 \(T\)에 비례하고, 몰질량(\(M\))에 반비례 한다는 것을 알 수 있습니다.
\[ \overline{v_{rms}^2} = \frac{3RT}{M} \]
근평균제곱속력(\(v_{rms}\))은 평균제곱속력(\(v_{rms}^2\))에 제곱근을 취한 것입니다.
\[ v_{rms} = \sqrt {\frac{3RT}{M}} \]
이와 같이 근평균제곱속력은 분자의 종류(분자량) 및 온도에 따른 함수로서 명확하게 정의될 수 있으며, 일정한 조건하에서 그 값이 변동하지 않습니다.
기체 분자의 평균 속력
평균 속력은 기체 분자의 속력을 산술 평균으로 계산한 값입니다. 두 분자가 충돌할 때 운동량은 보존되지만, 평균 속력은 계속 변동합니다. 기체 입자수가 충분히 많다고 가정한 평균 속력 < \(v\) >은 다음과 같습니다. (Maxwell-Boltzmann 확률분포식에서 유도됨, 유도과정 생략)
\[ < v > = \sqrt {\frac{8RT}{\pi M}} \]
평균 속력 < \(v\) >은 근평균제곱속력 \(v_{rms}\)보다 조금 작은 값을 가집니다.
그리고, 평균 속력은 일정한 값을 유지하지 않으며 조금씩 변화합니다. 분자 수가 적어질수록 변동이 더 심해집니다.