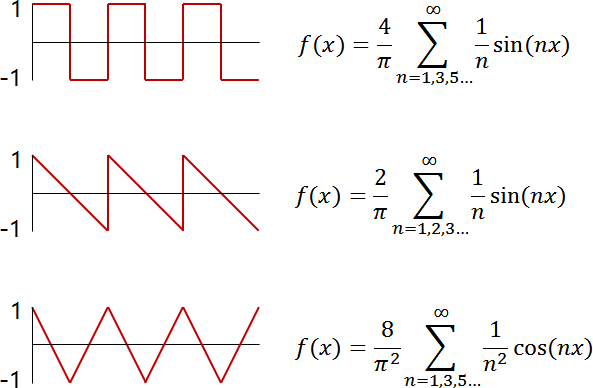푸리에 급수
푸리에 급수는 일정 부분이 반복되는 주기함수를 단순한 삼각함수의 합으로 표현하는 무한 급수를 말합니다.
단순한 삼각함수는 긴 파도의 너울처럼 부드러운 곡면으로 이루어져 있습니다. 이러한 삼각함수를 계속 더해 나가면 색다른 모양의 함수를 얻을 수 있습니다.
예를 들어 푸리에 급수를 이용하여 사각형 함수를 만들어 보겠습니다.
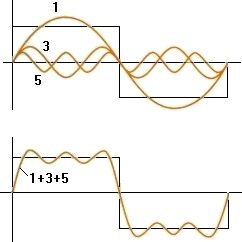
위 그림처럼 보통의 삼각함수를 3개 더하는 것으로 사각형 함수에 근접한 모양을 얻을 수 있습니다. 식으로 나열해 보면 다음과 같습니다.
\[ f(x)\, =\, sin(x)\, +\, \frac { 1 }{ 3 } sin(3x)\, +\, \frac { 1 }{ 5 } sin(5x) \]
지금은 3개의 함수만 더한 것이므로 완전한 사각형 모양이라고 하기에는 조금 부족합니다.
하지만 이런 식으로 무한히 더해 나갈 수 있다면 결국에는 깨끗한 함수꼴을 얻을 수 있습니다.
\[ \begin{align}
f(x)\, &=\, sin(x)\, +\, \frac { 1 }{ 3 } sin(3x)\, +\, \frac { 1 }{ 5 } sin(5x)\, +\,… \\
&=\, \sum _{ n=0 }^{ \infty }{ \frac { 1 }{ (2n+1) } sin((2n+1)x) }
\end{align} \]
푸리에 급수의 응용
푸리에 급수는 전자회로에서 특정한 파형을 얻고자 할 때 주로 사용됩니다.
예를들어 사각파와 톱니파에 대한 푸리에 급수식은 다음과 같습니다.
