Radioactive decay
The radioactive material can collapse its own nucleus structure. At the same time, the nucleus emits some small particles or energy to the outside. The emitted particles and radioactive energy can cause damage to the human body.
In 1895, the German physicist Röntgen detected X-rays, a kind of radiation. Röntgen discovered that when the X-ray is projected directly onto the living body, an image of the bone is formed on the photosensitive plate.

Among the early experimenters, Rutherford and colleagues found three components of radiation from radioactive materials. These components were called α, β, and r-ray. Later, those were identified as 'nuclei of helium atoms,' 'electrons,' and 'high energy photons.'
Half-life period
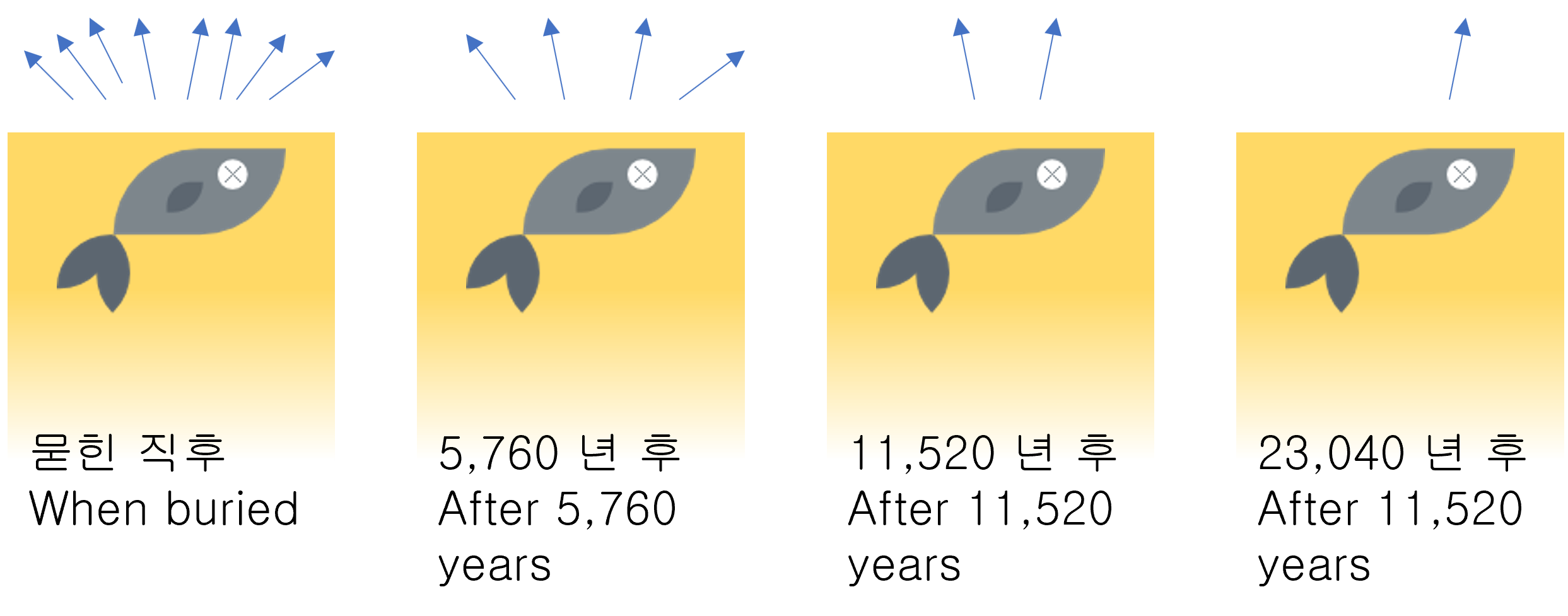
In radioactivity, Half-life is the interval of time required for one-half of a radioactive sample's atomic nuclei to decay.
If half-life passes again, half of the remaining mass will remain. (1/2, 1/4, 1/8, 1/16, 1/32, ...) The mass is getting smaller and smaller, but it always remains a bit.
\[ N(t) = N_0 {(\frac{1}{2})}^{\frac{t}{t_{1/2}}} \]
\(N(t)\): Mass after time t
\(N_0\): Mass at 't = 0' (initial mass)
\(t_{1/2}\): Half-life period
Radiometric dating
Since radioactive decay proceeds at a constant rate irrespective of external conditions, we can measure the samples' age.