전지와 부하
전기 회로에서 전지는 전압차를 유지하여 회로에 전류가 흐를 수 있도록 합니다.
전지가 만들어낸 전압차에 의해 전류가 흐르면서 에너지를 소비하게 되는데, 에너지가 소비되는 곳을 부하라고 부릅니다. 보통 학교 실험실에서 부하는 꼬마전구 또는 저항이 됩니다.
모든 전기 회로에서 전압은 올라간 만큼 내려갑니다. 올라간 높이와 내려간 높이를 수치로 나타낼 수 있다면 올라간 높이와 내려간 높이의 합은 ‘0’이 됩니다. 이것은 놀이공원의 롤러코스터를 생각하면 쉽습니다. 롤러코스터를 타면 처음에는 높은 곳으로 올라갑니다. 그 다음 롤러코스터는 밑으로 쭉 내려가면서 짜릿함을 즐기게 됩니다. 롤러코스터가 중간에 오르락 내리락 하더라도 내려갔던 전체 높이는 올라갔던 전체 높이와 같습니다.
저항의 직렬 연결
저항 두 개를 직렬 연결할 경우, 저항은 각각의 전압을 나누어 가져가게 됩니다. 이 경우 각각의 저항에 걸리는 전압은 원래 전압보다 작아집니다. 두 개의 저항에 걸리는 전압을 모두 더해야 원래의 전압이 됩니다.
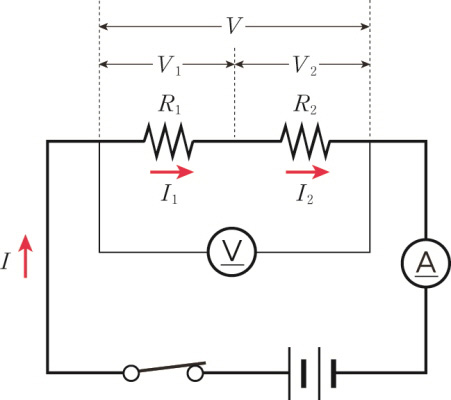
두 저항이 직렬로 연결되어 있을 때 각 저항에 흐르는 전류는 전체 회로에 흐르는 전류의 세기와 같습니다.
\[ I\; =\; { I }_{ 1 } \; = \; { I }_{ 2 } \]
한편, 회로에 걸어 준 전체 전압 V는 두 저항에 나누어져 걸리므로, 각 저항에 걸리는 전압의 합은 전체 전압과 같습니다.
\[ V\; =\; { V }_{ 1 }+{ V }_{ 2 } \]
전체 회로에 흐르는 전류의 세기를 I라 하면, 옴의 법칙으로부터 V1 =IR1, V2 =IR2 가 됩니다.
회로의 전체 저항을 합성 저항 R이라 하면 옴의 법칙으로부터 V =IR이므로 다음과 같은 관계가 성립합니다.
\[ V\; =\; { V }_{ 1 }+V_{ 2 }\; =\; I{ R }_{ 1 }+I{ R }_{ 2 }\; =\; I({ R }_{ 1 }+{ R }_{ 2 }) \]
\[ \therefore \; R\; =\; { R }_{ 1 }+{ R }_{ 2 } \]
즉, 두 저항이 직렬로 연결되어 있을 때 합성 저항은 각 저항을 합한 것과 같습니다. 따라서 저항을 직렬로 연결할수록 합성 저항은 커집니다.
저항의 병렬 연결
저항 두 개를 병렬 연결한 경우, 각각의 저항에 걸리는 전압은 원래의 전압과 같습니다. 병렬 연결된 저항은 그 개수가 몇 개이든 간에 저항에 걸리는 전압은 원래의 전압과 같습니다.
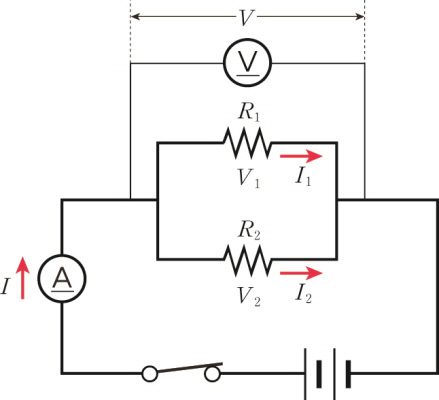
두 저항이 병렬로 연결되어 있을 때 각 저항에 흐르는 전류의 합은 전체 회로에 흐르는 전류의 세기와 같습니다.
\[ I\; =\; { I }_{ 1 }+{ I }_{ 2 } \]
한편, 두 저항이 다른 저항을 거치지 않고 직접 전원에 연결되어 있으므로, 각 저항에 걸리는 전압은 전체 전압과 같습니다.
\[ V\; =\; { V }_{ 1 } \; = \;V_{ 2 } \]
회로에 걸리는 전압을 V라 하면, 옴의 법칙으로부터 I1 = V / R1, I2 = V / R2 가 됩니다.
회로의 전체 저항을 합성 저항 R이라 하면 옴의 법칙으로부터 I = V / R 이므로 다음과 같은 관계가 성립합니다.
\[ I\; =\; { I }_{ 1 }+{ I }_{ 2 }\; =\; \frac { V }{ { R }_{ 1 } } +\frac { V }{ { R }_{ 2 } } \; =\; V(\frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } ) \]
\[ \therefore \; \frac { 1 }{ R } \;=\; \frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } \]
즉, 두 저항이 병렬로 연결되어 있을 때 합성 저항의 역수는 각 저항의 역수의 합과 같습니다. 따라서 저항을 병렬로 연결할수록 합성 저항은 작아집니다.