ヤングの二重スリット





 

スリットの間隔と位置を調整することができます。

ヤングの二重スリット実験

Youngの干渉実験は、以下のとおりです。
スクリーン「A」の小さな穴 ‘S0」で回折された光が、スクリーン「B」にある小さな穴’ S1」と「S2」を通過されます。二つの小さな穴を過去の光が、スクリーン「B」と「C」の間で重ね合わせになり、スクリーン「C」の干渉縞を作成します。

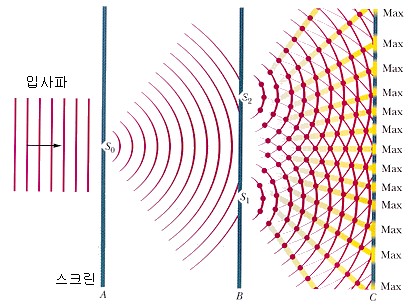
二つのスリットから到着した波の位相が同じ場合、明るい柄が生じ、位相が同じでない波が重なるとき、黒柄が生じます。

補強干渉

スクリーンで同じ位相に到達する部分は「補強干渉」が起きて明るく見えます。
補強干渉を起こすためには、經路差であるd・sinθが「0」または波長の整数倍が必要です。

補強干渉（極大） \( d\cdot sin(\theta )\,=\,n\lambda \) (n = 0, 1, 2…)

極大位置 \( { y }_{ n }\,=\,\frac { n\lambda D }{ d } \) (n = 0, 1, 2…)

d: スリットの間隔(m)
θ: 回折角(rad)
λ: 光の波長(m)
D: スリットからスクリーンまでの距離(m)

「n=0」のとき、中心軸回折角「θ=0」です。結局中心軸は、スクリーンの中心にあります。

相殺干渉

スクリーンで暗い地域では、「相殺干渉」が起こります。
相殺干渉を起こしためには、二つの光の経路差が半波長の奇数倍である必要があります。

相殺干渉（極小） \( d\cdot sin(\theta )\,=\,(n+\frac { 1 }{ 2 } )\lambda \) (n = 0, 1, 2…)

極小の位置 \( { y }_{ n }\, =\, \frac { \left( n+\frac { 1 }{ 2 } \right) \lambda D }{ d } \) (n = 0, 1, 2…)

d: スリットの間隔(m)
θ: 回折角(rad)
λ: 光の波長(m)
D: スリットからスクリーンまでの距離(m)

上記の「n」の値は、相殺干渉による暗い模様に番号を付けるときに使用します。